Factorisation $LU$

On factorise 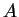$A$ en un produit d'une matrice triangulaire inférieure $L$ et d'une matrice triangulaire supérieure $U$, autrement dit $A=LU$. Cela permet une résolution numérique plus facile en deux étapes. La première étape consiste à résoudre le problème :

$$Lx'=b ;$$

la seconde étape à résoudre le problème :

$$Ux=x'.$$

Le vecteur $x$ est alors solution de l'équation (1).

function [L,U]=facLU(A)
// Factorisation LU d'une matrice inversible A
//
U=zeros(A);
L=eye(A);
//
U(1,:)=A(1,:);
//
dimmat=size(A,'r');
//
for i=2:dimmat
    for j=1:i-1
        L(i,j)=(A(i,j)-L(i,1:j-1)*U(1:j-1,j))/U(j,j);
    end
    for j=i:dimmat
        U(i,j)=A(i,j)-L(i,1:i-1)*U(1:i-1,j);
    end
end
endfunction