



suivant: Programmation Dynamique
monter: Quelques méthodes numériques en
précédent: Méthode de la Section
Table des matières
Étant donné une fonction
 et
et
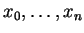
 points dans
points dans
 . Lagrange à résolu le problème de déterminer le
polynome
. Lagrange à résolu le problème de déterminer le
polynome 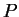 vérifiant :
On montre que ce polynome
vérifiant :
On montre que ce polynome 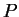 s'écrit sous la forme suivante :
avec :
s'écrit sous la forme suivante :
avec :
![$\displaystyle f[x_i]=f(x_i),\quad f[x_i,\ldots,x_{i+k+1}]=\frac{f[x_{i+1},\ldots,x_{i+k+1}]-f[x_i,\ldots,x_{i+k}]}{x_{i+k+1}-x_i}.$](img27.png) |
(2) |
Nous allons ranger les éléments
![$ f[x_i,\ldots,x_{i+k+1}]$](img28.png) dans une
matrice
dans une
matrice 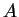 de la manière suivante :
de la manière suivante :
- l'indice de ligne sera l'indice du dernier terme dans le crochet
![$ [x_i,\ldots,x_{i+k+1}]$](img29.png) auquel on rajoute
auquel on rajoute 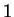 c'est-à-dire
c'est-à-dire
 ;
;
- l'indice de colonne correspond au nombre d'éléments entre le
crochet
![$ [x_i,\ldots,x_{i+k+1}]$](img29.png) c'est-à-dire
c'est-à-dire 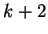 .
.
Autrement dit
![$ A(i+k+2,k+2)=f[x_i,\ldots,x_{i+k+1}]$](img33.png) . En notant
. En notant
![$ points=[x_0,\ldots,x_n]$](img34.png) (
(
 ), l'équation
(2) devient :
On procède alors à un changement de variable en posant
), l'équation
(2) devient :
On procède alors à un changement de variable en posant  et
et
 il vient donc :
Pour des raisons d'efficacité nous avons programmé deux fonctions. La
première calcule la matrice
il vient donc :
Pour des raisons d'efficacité nous avons programmé deux fonctions. La
première calcule la matrice 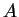 , la seconde calcule le polynome
, la seconde calcule le polynome 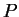 en
utilisant
en
utilisant 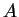 .
.
function [y]=interpolation(x,d,points)
// Polynome d'interpolation de Lagrange d'une fonction f
n=size(points,'*')
y=d(1)
T=x-points(1);
for i=2:n
y=y+d(i)*T;
T=T*(x-points(i));
end
endfunction
function [d]=prepross(f,points)
n=size(points,'*')
A=zeros(n,n);
for k=1:n
A(k,1)=f(points(k));
end
d(1)=A(1,1);
for j=2:n
for i=j:n
A(i,j)=(A(i,j-1)-A(i-1,j-1))/(points(i)-points(i-j+1));
end
d(j)=A(j,j);
end
endfunction
L'exemple suivant montre le résultat en bleue de l'interpolation de la fonction
 en rouge aux points
en rouge aux points
![$ [0 0.5 1 1.5 2]$](img41.png)
Figure:
Interpolation de Lagrange de la fonction 
|
|




suivant: Programmation Dynamique
monter: Quelques méthodes numériques en
précédent: Méthode de la Section
Table des matières
barty
2004-04-29
![$\displaystyle P(x)=f[x_0]+\sum_{j=1}^{n}f[x_0,\ldots,x_j]\Pi_{i=0}^{j-1}(x-x_i) ;
$](img26.png)

